How to find the starting point of a loop in a linked list.
It is based on Floyd’s algorithm for cycle detection.
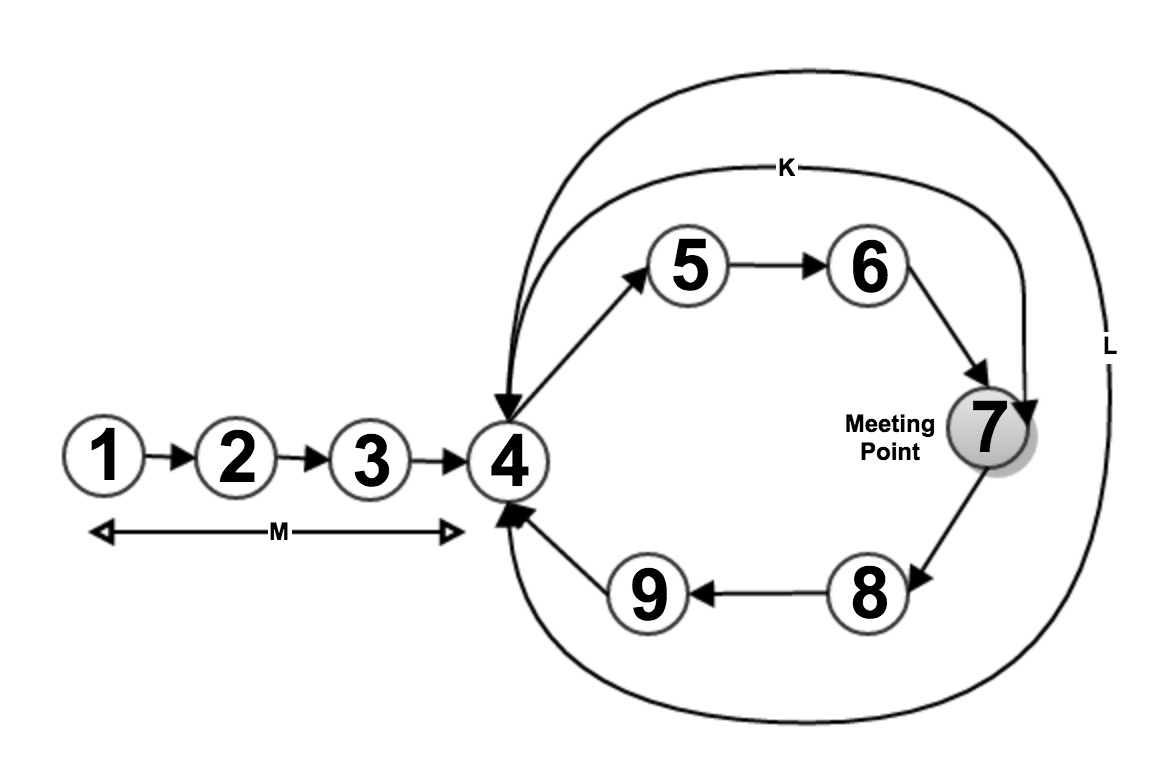
First we try to find out, is there any loop in list or not. If loop exists then we try to find out starting point of loop. For this we use two pointers namely slowPtr and fastPtr. In first detection (checking for loop), fastPtr moves two steps at once but slowPtr moves by one step ahead at once.
Example:
| slowPtr | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| fastPtr | 1 | 3 | 5 | 7 | 9 | 5 | 7 |
It is clear that if there is any loop in list then they will meet at point (Point 7 in above image), because fastPtr pointer is running twice faster than other one.
Now, we come to second problem of finding starting point of loop.
Suppose, they meet at Point 7 (as mentioned in above image). Then, slowPtr comes out of loop and stands at beginning of list means at Point 1 but fastPtr still at meeting point (Point 7). Now we compare both pointers value, if they same then it is starting point of loop otherwise we move one step at ahead (here fastPtr is also moving by one step each time) and compare again till we find same point.
| slowPtr | 1 | 2 | 3 | 4 |
| fastPtr | 7 | 8 | 9 | 4 |
Now one question comes in mind, how is it possible. So there is good mathematical proof.
Suppose:
m => length from starting of list to starting of loop (i.e 1-2-3-4) l => length of loop (i.e. 4-5-6-7-8-9) k => length between starting of loop to meeting point (i.e. 4-5-6-7) Total distance traveled by slowPtr = m + p(l) +k where p => number of repetition of circle covered by slowPtr Total distance traveled by fastPtr = m + q(l) + k where q => number of repetition of circle covered by fastPtr Since, fastPtr running twice faster than slowPtr Hence, Total distance traveled by fastPtr = 2 X Total distance traveled by slowPtr i.e m + q(l) + k = 2 * ( m + p(l) +k ) or, m + k = q(l) - p(l) or, m + k = (q-p) l or, m = (q-p) l - k So, If slowPtr starts from beginning of list and travels "m" length then, it will reach to Point 4 (i.e. 1-2-3-4) and fastPtr start from Point 7 and travels " (q-p) l - k " length then, it will reach to Point 4 (i.e. 7-8-9-4), because "(q-p) l" is a complete circle length with " (q-p) " times.
Source code:
Github: LoopDetector.java
Output:
[1=>2, 2=>3, 3=>4, 4=>5, 5=>6, 6=>7, 7=>8, 8=>9, 9=>4, ] Loop Starting point : ListNode(4)