Find largest rectangle in histogram.

Given an array with heights (all non-negative) of rectangle (assuming width is 1), we need to find the largest rectangle area possible.

There are various solution for this.
Let’s discuss about solution:

There are a lot of solutions for this, one of them are given by Judges. I will show three different approaches to solve this. Let’s start with simpler whose run time is O(n²).

Suppose we have an array with height for histogram bars (for simplicity width of each bar is 1).

Solution 1:

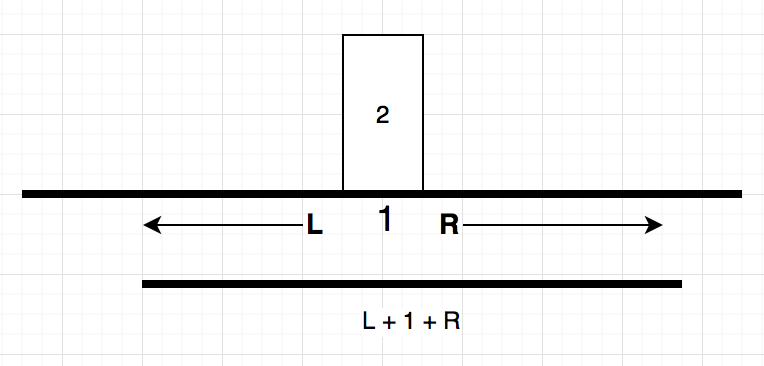
(As shown in above image).
Now, for every i element of array, we have to calculate area, i.e.

Area of rectangle = Height * Wight
So,
A(i) = H(i) * W(i)
    where i >=0 to i < array.length

And in all A(i)s, we have to find out max one.

Now we come to H(i) and W(i),

H(i) is the height of bar means,
H(i) = Array[i]

But for W(i),
W(i) = L(i) + R(i) + 1

Where,
L(i) => Number of bars adjacent to left of ith node whose height is greater than of equal to height of i bar.
H(i) => Number of bars adjacent to right of ith node whose height is greater than or equal to height of i bar.

Now check the method calculateAreaInNonLinearTime() which doing same thing.

• Its calculating L(i) for every i element.
• Then calculating R(i) for every i element.
• Then area A(i)  = H(i) * [L(i) + R(i) + 1]
• And the finding max area in A(i).

Complexity:

Finding L(i) = O(n²)
Finding R(i) = O(n²)
Calculating A(i) = O(n)
Finding max A(i) = O(n)
Final complexity is O(n²) + O(n²) + O(n) + O(n) = O(n²)

But we can optimize this, see in next solution.

Solution 2:

In this solution we will use stack to find L(i), which reduces complexity for finding L(i) from O(n²) to O(n).  Check method: calculateAreaInLinearTime().

Steps: coming soon……….

Solution 3:

Setups of this solutions are:

• For this solution we are using two different stacks, one for storing height and another for start position of that height.
• We move from left to right
  • if stack is empty then, then push height and index in respective stacks.
  • If stack is not empty and current height is greater than previous height (i.e. array[i] > heightStack.top()), then push height and index in respective stacks.
  • If stack is not empty, but current height is smaller than previous height (i.e. array[i] > heightStack.top()), then do following things:-
    • take height = heightStack.pop(),
    • take width = i – startPositionIndexStack.pop
    • Calculate Area = height * width
    • if area > maxArea then, maxArea = area.
    • Repeat these steps until stack is not empty and array[i] > heightStack.top().
    • After that push height to height stack and last start position to position stack.
  • Increase loop counter and repeat until all items in array not consumed.
• If stack is still not empty, then do following this.
  • take height = heightStack.pop(),
  • take width = i – startPositionIndexStack.pop
  • Calculate Area = height * width
  • if area > maxArea then, maxArea = area.
  • Repeat this till stack is not empty.

Continue……….

Check code: calculateArea3()
Source Code:
Github: LargestRectangleHistogram.java

Output:

 
largest rectangle area1 (non-linear): 7
largest rectangle area2 (linear): 7
largest rectangle area3 (linear): 7

largest rectangle area1 (non-linear): 9
largest rectangle area2 (linear): 9
largest rectangle area3 (linear): 9

largest rectangle area1 (non-linear): 10
largest rectangle area2 (linear): 10
largest rectangle area3 (linear): 10

Video